«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и графики способны заменить нам долгие разъяснения.
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.
Пример. Известны координаты пятнадцати точек: А(4, 1), В(4, 2), С(1, 2), D(4, 5), Е(2, 5), F(4, 7), G(3, 7), Н(5, 9), 1(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А—В—С—D—Е—F—G—Н—I—J—К—L— М — N — О — А, то получим следующий рисунок:
Любая, в том числе и графическая, информация может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них — числовую ось — вы уже рассматривали на уроках математики.
Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.
Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе — по оси OY. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси OY).
Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.
Пример. Известны координаты пятнадцати точек: А(4, 1), В(4, 2), С(1, 2), D(4, 5), Е(2, 5), F(4, 7), G(3, 7), Н(5, 9), 1(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А—В—С—D—Е—F—G—Н—I—J—К—L— М — N — О — А, то получим следующий рисунок:
Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.
С методом координат можно познакомиться в презентации.
С методом координат можно познакомиться в презентации.
Самое главное
Рисунки, схемы, чертежи, графики — графические формы представления информации. Метод координат — это один из удобных способов представления графической информации с помощью чисел.
Вопросы и задания
1. Что такое метод координат? Расскажите о нём.
2. Как метод координат применяется в географии?
3. Где вы сталкиваетесь с методом координат в быту?
4. Известны ли вам игры, основанные на методе координат? Об одной из таких игр можно прочесть в § 3.7.
5. На координатной плоскости отметьте и пронумеруйте точки со следующими координатами: А(2,5), В(6,5), C(11,7), D(11,4), Е(6,2), F(2,2), G(4,8), Н(9,9),
6. Соедините точки: А — В — С — D — Е — F — A — G — Н — С. G — В — Е. I — J — К — L.
После проверки правильности выполнения задания можно раскрасить полученную картинку цветными карандашами.
7. Игра «Шифровальщик». Выполните действия по следующему плану:
1) на листочке в клетку нарисуйте произвольный многоугольник;
2) пронумеруйте его вершины и закодируйте их с помощью координат;
3) задайте порядок соединения вершин;
4) проверьте, не допущена ли вами ошибка при кодировании рисунка;
5) координаты точек и порядок их соединения выпишите на отдельный листок;
6) предложите кому-нибудь восстановить ваш рисунок по этому коду;
сравните результаты — возможно искажение информации при декодировании.


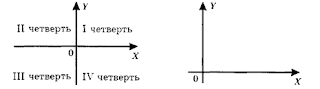

Комментариев нет:
Отправить комментарий